Jak policzyć opór cewki

[mbar]

Tylko że we wzorach na filtr nie bierze się indukcyjności cewki głośnika . to nie trzyma się kupy

Kupy to się nie trzyma Twoja matematyka :)
Zastanów się nad tym wzorem (to, że tam jest C to szczegół):


Poanalizuj taki obwód:



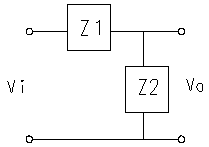
Dlaczego w jednym wzorze są "pałki", a w drugim nie?
Przyjmij Vi = 1 V, Vo = 0,707 V :)

[Yoshi_80]

Tylko że we wzorach na filtr nie bierze się indukcyjności cewki głośnika . to nie trzyma się kupy

Nie trzyma się kupy dla ciebie bo ty chcesz zastosować ten wzór do konkretnej wąskiej dziedziny jaką jest głośnik a filtry są urzędzeniem uniwersalnym, fitlrowac można nie tylko sygnały akustyczne ze wzmacniacza do głośnika .

Ten wzór można oczywiście przerobić i uwzględnić indukcyjnośc głośnika ale byłby to straszny błąd. Filtr obliczany jest dla rezystancji i dla rezystancji otrzymujesz założone parametry filtru (częstotliwość filtracji, charakterystyke filtracji itd ) generalnie, dla rezystancji otrzymujesz modelową filtrację.

Po uwzględnieniu we wzorze indukcyjności i obliczeniu fitlru, jedyny parametr tego filtru jaki by się zgadzał to chyba tylko punkt -3dB filtru a cała reszta parametrów byłaby tragiczna.
Nie wiem czy czytałeś tego mojego arta http://diyaudio.pl/content.php/45-Teoria-filtrow ale może cię zainteresować ostatni jego punkt gdzie masz przeprowadzone symulacje filtru licznonego teoretycznie na rzeczywistym obciążeniu (czyli głośniku).

Nawet jak uwzględnisz indukcyjność w wartości impedancji dla filtru w obliczeniach to jest to droga do nikąd.

A uwzględnianie tego "j" w obliczeniach dużo daje bo matematyka liczb zespolonych jest inna od klasycznej i nie można liczyć liczb zespolonych wiedzą ze szkoły średniej bo wyjdą głupoty .

Nie na temat...

Skoro przytaczamy anegdoty to i ja napiszę jedną z własnego studenckiego życia. Mieliśmy naprawdę fajnego (jak się później okazało), uznanego w świecie nauki (bo gościa wiecznie nie było, ciągle na jakiś zagraniczncyh wyjazdach), profesora od fizyki. Na 1 roku miałem z nim poza wykładem ćwiczenia, był to poczatek roku akademickiego. Pan profesor rzuca na tablice zadanko i pyta czy ktoś chce rozwiązać. Widzę, że wszyscy cicho siedzą i chyba nic nie kumają a ja pasjonat fizyki, obryty po szkole średniej bo i w olimpiadach próbowałem sił, to się zgłaszam. W parę chwil rozpykuję to zadanko swoimi metodami z LO, zadowolony z siebie siadam. Pan profesor patrzy krytycznym okniem i rzuca "co pan tu napisał !". Podchodzi, zmazuje moje wypociny, robi to po swojemu czyli wytacza cieżkie działa, wali całki, różniczki itd, same banalne, oczywiste, wręcz trywialne dla młodego studenciaka rzeczy, w mgnieniu oka rozwala zadanie i.. ma ten sam wynik co ja :thumbsup: POmimo jednakowych wyników oczywiście wiadomo kto miał racje .

[mbar]

Filtr obliczany jest dla rezystancji

No bo tylko część rzeczywista impedancji wykonuje użyteczną pracę, czyli "gra" :)
Dlatego "olaboga" bo kolega Amadeus raz sobie bierze Z, raz R i jakby nie klepał, to zawsze mu przystanek wyjdzie.

[Amadeus11]

Wiem do czego są te palki we wzorach i jak sie je liczy . y=|x| , y={ x dla x>0 , -x dla x<0 }
tylko nie wiem jak policzyc te -3dB.

Chciałbym by ktoś napisał algorytm dla cewki szeregowej z głośnikiem wtedy bym go przeanalizował dokładnie. Potem bym próbował go rozbudować o następne rzędy filtru.

[mbar]

Wiem do czego są te palki we wzorach i jak sie je liczy . y=|x| , y={ x dla x>0 , -x dla x<0 }

Sorry, ale nie wiesz :)
Działamy na liczbach zespolonych, a nie rzeczywistych. Pierwiastek z sumy kwadratów!

[Amadeus11]

Sorry, ale nie wiesz :)
Działamy na liczbach zespolonych, a nie rzeczywistych. Pierwiastek z sumy kwadratów!

Liczbą zespoloną jest ( i ), a nie pałki . Pałki to wartość bezwzględna.

---------- Post dodany o 17:23 ---------- Poprzedni post o 16:50 ----------

Muszę to ogarnąć http://pl.wikipedia.org/wiki/Cewka
http://pl.wikipedia.org/wiki/Liczby_zespolone

[mbar]

I rest my case...

Sent from my GT-N7000 using Tapatalk

[raven1985]

O rety ! (Jak by powiedział pewien głupiutki miś :) )
Ciężka sprawa. Ja liczby zespolone miałem na elektrotechnice jeszcze w technikum i to 2 jego klasie. Śmieszne bo wtedy nikt nie słyszał nawet o czymś takim jak pochodna :biggrin:
Ja może nieco bardziej jestem na bieżąco chociaż gdy by mi ktoś kazał liczyć to ręcznie to bym go chyba powiesił :biggrin: Się w życiu studenckim już wytaczającą naliczyłem. Teraz mam komputer i on brudną robotę odwala.
Ta matematyka to tylko narzędzie i tak trzeba ją traktować. O filtrach znam kilka książek jednak są to już pozycję dla wtajemniczonych i po angielsku od których można dostać napadowego ziewania Wytłumaczenie o co chodzi z tym "j" nie jest łatwe ale i nie jest konieczne do zrozumienia tego wszystkiego jak i ta cała matematyka w którą tu kolega z uporem maniaka brnie :) myląc na dodatek pojęcia, moc z -3dB itp.
Polecam koledze rozejrzenie się na E-portalu i w archiwum EdW :) http://www.elportal.pl/ Jak dobrze się rozejrzysz na pewno znajdziesz to czego szukasz i przystępnej formie :)

[Yoshi_80]

Amadeus11 ale co chcesz osiągnąć ? Bo chyba chcesz na siłę udowodnić wszystkim swoje racje.

Próbujesz uczyć matematyki ludzi którzy pokończyli studia i wielokrotnie liczyli na liczbach zespolonych, sam nie mając o tym zielonego pojęcia. Próbujesz udowodnić to, że filtr powinien mieć -10dB zamiast -3dB skoro od zawsze jest tak, że filtr wylicza się na punkt -3dB. Nie wiadomo po co tworzysz jakieś dziwne teorie. Chcesz udowodnić, ze wszyscy się mylą?
To ci się nie uda, chociażby dlatego, że nikt tu się nie zajmuje wzorami na filtr, nikt niczego nie oblicza, nie tworzy filtrów na drodze teoretycznej bo to jest zupełnie zbędne. Sposobem w jaki podchodzisz do tematu nie osiągniesz wymiernych rezultatów w postaci dobrze zaprojektowanych filtrów zwrotnicy.

[Amadeus11]

Amadeus11 ale co chcesz osiągnąć ? Bo chyba chcesz na siłę udowodnić wszystkim swoje racje.

Próbujesz uczyć matematyki ludzi którzy pokończyli studia i wielokrotnie liczyli na liczbach zespolonych, sam nie mając o tym zielonego pojęcia. Próbujesz udowodnić to, że filtr powinien mieć -10dB zamiast -3dB skoro od zawsze jest tak, że filtr wylicza się na punkt -3dB. Nie wiadomo po co tworzysz jakieś dziwne teorie. Chcesz udowodnić, ze wszyscy się mylą?
To ci się nie uda, chociażby dlatego, że nikt tu się nie zajmuje wzorami na filtr, nikt niczego nie oblicza, nie tworzy filtrów na drodze teoretycznej bo to jest zupełnie zbędne. Sposobem w jaki podchodzisz do tematu nie osiągniesz wymiernych rezultatów w postaci dobrze zaprojektowanych filtrów zwrotnicy.

Ale dzieki temu tematowi zobaczyłem ze nie wiem wszystkiego o liczbach zespolonych i obliczaniu tych wzorów . Myslałem ze to tylko zank minus trzeba do wyniku dostawic . Teraz juz sie douczyłem troche i wiem ze zamiast ( j ) podstawia sie pierwiastek z minus jeden . A jezeli chodzi o nazwy to są dwie . dla tych kresek pionowych jest nazwa oddzielana a dla litery (j) jest oddzielna . Sprawdziłem w książce :)

Ja chcę zrozumiec gdzie popełniam bład w obliczeniu cewki , nie chcem udowadniac swoich racji bo wiem ze sie mylę . A jęzeli myslicie ze chcę potem za pomocą tego obliczyć filtr to się mylicie. Nawet program tego nie potrafi dobrze zrobić podstawiając więcej danych niż ja bym podstawił w tym filtrze . To było tylko pytanie czysto teoretyczne .

[Yoshi_80]

Myslałem ze to tylko zank minus trzeba do wyniku dostawic . Teraz juz sie douczyłem troche i wiem ze zamiast ( j ) podstawia sie pierwiastek z minus jeden . A jezeli chodzi o nazwy to są dwie . dla tych kresek pionowych jest nazwa oddzielana a dla litery (j) jest oddzielna . Sprawdziłem w książce

Próbujesz sposobem rozumowania z poziomu szkoły średniej ugryźć liczby zespolone, tak się nie da. Za j niczego się nie podstawia, j to j, oznacza częśc urojoną liczby zespolonej. j eliminuje się gdy np wyliczasz moduł tej liczby (czyli np impedancję która jest modułem liczy zespolonej złożonej z rezystancji (częśc rzeczywista) i admitancji (część urojona)). Nie można tak po prostu sobie "kasować" tego j'ta bo on ci się nie podoba więc od razu chcesz sie go pozbyć.

[pegelmesser]

j jest stałą i wynosi 1 a czasem -1 , tego się nie oblicza. To taki twór matematyczny i stosuje się go do tego aby oznaczyć urojoną część liczby zespolonej. j zaprzecza całej matematyce do poziomu szkoły średniej włącznie bo pierwiastek z j = -1 , coś co szkole średniej było "niemożliwe".

Eee.. j to jest (-1) do potegi 1/2 czyli pierwiastek z -1.
Nic w tym zaskakujacego ani wielce dziwnego. Liczby urojone i zespolone maja czyste przelozenie na zjawiska fizyczne. Niestety ludzie ograniczenie nie potrafia połączyć pewnych rzeczy w jedna calosci mysla ze matematyka to jakas dziwna teoria i sklada sie z wielu roznych niezwiazanych ze soba wzorow, dzialow itp.
Ale ja i tak wole liczy przy pomocy http://pl.wikipedia.org/wiki/P%C5%82aszczyzna_S oraz http://pl.wikipedia.org/wiki/Transformata_Laplace%27a gdzie od razu widze co i jak z biegunami ukladu i stabilnoscia oraz przebiegiem charakterystyki.

[raven1985]

Koncepcja jest prosta. Zamiast rozwiązywać równania różniczkowe zamienia się je na algebraiczne. łatwiej dodawać niż całkować :) Dla przebiegów sinusoidalnych j dla dowolnych s.

[pegelmesser]

A jeszcze lepiej zapuscic program co policzy wszsytko sam i nie trzeba sie martwi... ale oczywiscie trzeba wiedziec co robi ijak wyniki interpertowac i tu wracamy do podstaw...

[raven1985]

Bajka o liczbach zespolonych :)
http://www.elportal.pl/pdf/k01/19_06.pdf
http://www.elportal.pl/pdf/k01/20_08.pdf