-
Witamy w największym polskim serwisie internetowym poświęconym w całości zagadnieniom samodzielnej budowy nagłośnienia.
Dzięki DIYaudio.pl poznasz zagadnienia samodzielnej budowy nagłośnienia od podszewki oraz będziesz mógł dyskutować o DIY audio do woli.
Artykuły z dawnego portalu zostały przeniesione do sekcji forum na samym dole.
Projekt zwrotnicy do zestawu głośnikowego w obudowie ALTUS 300
- Autor wątku KRASUL
- Data rozpoczęcia
Tak niskie częstotliwości podziału stosuje się raczej w dwudrożnych monitorach studyjnych małej mocy. W bieżącym projekcie priorytetem było przydzielenie głośnikowi średniotonowemu możliwie szerokiego zakresu pracy w paśmie przepustowym. Obejmuje on całą dekadę (500 Hz - 5000 Hz). Ważne było też zgranie fazowe, odpowiedni podział mocy zabezpieczający głośniki przed przeciążeniem oraz wypadkowa charakterystyka modułu impedancji w funkcji częstotliwości umożliwiająca współpracę z dowolnym rodzajem wzmacniacza. Głośnik GDM 18/80 to bardzo dobry i wytrzymały przetwornik. Niestety w oryginalnych Altusach 300 jest on filtrowany filtrem pasmowoprzepustowym pierwszego rzędu bez żadnej kompensacji i dzięki temu gra jak megafon. Filtr pasmowoprzepustowy trzeciego rzędu w konfiguracji typu "T" z tłumieniem i kompensacją pozwala efektywniej wykorzystać zalety tego głośnika. Mało który głośnik wysokotonowy Tonsilu wytrzyma za filtrem więcej niż 1,5 - 2,5 W RMS. A to narzuca zastosowanie nieco wyższej częstotliwości podziału i koło się zamyka...
Ostatnia edycja:
KRASUL wpadnij na spota -> https://diyaudio.pl/forum/na-luzie/zbiorowe-zam-wienia/646191-spot-forumowy-2022
Fajny klimat, techniczne pogaduchy, jedzenie, nocleg - poznasz szyderców ;p
Trochę sprzętu.
Zapisz się.
Super impreza.
Fajny klimat, techniczne pogaduchy, jedzenie, nocleg - poznasz szyderców ;p
Trochę sprzętu.
Zapisz się.
Super impreza.
Dziękuję za zaproszenie. Tak teraz myślę, że można by też podejść do tematu w sposób nieszablonowy i spróbować "zmusić" oryginalny głośnik GDWT 9/100 FP do pracy z tak niską częstotliwością podziału. Jego cewka jest chłodzona w szczelinie powietrznej ferrofluidem co zwiększa wytrzymałość mocową. Efektywność tego głośnika i tak trzeba by obniżyć o 10 dB SPL dzielnikiem oporowym, dzięki czemu głośnik byłby dodatkowo zabezpieczony przed przeciążeniem. Wadą takiego rozwiązania byłaby jednak bardzo duża kierunkowość emisji sygnału wynikająca z faktu, że jest to głośnik tubowy. Zaletą byłoby zachowanie wyglądu zewnętrznego oryginalnego zestawu Altus 300 oraz możliwość skorzystania z fabrycznego pierścienia dekoracyjnego (w przypadku GDWK 9/80/1 taki pierścień trzeba sobie dorobić).
Kiedys myslalem nad zrobieniem projektu Altus ale z wykorzystaniem GDWT 12/19, ktory wg mnie jest lepszym wyborem niz GDWT 9/100, poniewaz ma lepsze charakterystyki katowe, a duzy horn mocniej obciaza glosnik, dzieki czemu mozna zejsc z podzialem nizej, bez obawy o uszkodzenie cewki. Z wycieciem otworu pod ten glosnik nawet amator nie powinien miec klopotu, bo nie trzeba do tego frezarki.
Na innym forum powstal nawet taki projekt oversize z tym tweeterem oraz GDN 30/60/1
Chociaz nie wiem czy ten tweeter zmiesci sie w oryginalna obudowe Altusa. Trzeba by bylo to pomierzyc.
Na innym forum powstal nawet taki projekt oversize z tym tweeterem oraz GDN 30/60/1
Chociaz nie wiem czy ten tweeter zmiesci sie w oryginalna obudowe Altusa. Trzeba by bylo to pomierzyc.
Ostatnia edycja:
Tonsil po dzień dzisiejszy produkuje tego typu zestaw głośnikowy ZEUS:
Pokaż załącznik ZGB_200-4-566_ZEUS.PDF
1 x GDWT 12-19/100 + 2 x GDN 30/120
Zestaw jest dwudrożny. GDN-y są połączone równolegle i pracują bez filtracji w obudowie basrefleks natomiast GDWT ma filtr drugiego rzędu i żarówkę samochodową 12V/21W przed filtrem.
Pokaż załącznik ZGB_200-4-566_ZEUS.PDF
1 x GDWT 12-19/100 + 2 x GDN 30/120
Zestaw jest dwudrożny. GDN-y są połączone równolegle i pracują bez filtracji w obudowie basrefleks natomiast GDWT ma filtr drugiego rzędu i żarówkę samochodową 12V/21W przed filtrem.
Zeus to jednak nieco inna konstrukcja, przeznaczona do zupelnie innego odbiorcy. Jednak daje ona pewien poglad o mozliwosciach ciecia GDWT, dlatego mysle, ze moglby sie bardzo dobrze spasowac z GDM 18.
Korzystając z okazji przesyłam linka do strony internetowej rumuńskiego przedstawicielstwa handlowego Tonsilu, na której można znaleźć karty katalogowe głośników, których nie ma na stronie polskiej:
https://tonsil.ro/Drivers.htm
https://tonsil.ro/Drivers.htm
Według karty katalogowej zastosowany w PAŃSKIM projekcie GDWK 9/80/1 ma rezonans na poziomie 1100 hz co jak na przetwornik bez komory rezonansowej jest wynikiem bardzo dobrym wobec czego ponawiam pytanie - co stało na przeszkodzie przesunięcia podziału niżej w celu eliminacji "break-upu " GDM-a tylko proszę sobie darować te wywody na temat liniowego modułu impedancji w funkcji częstotliwości, bo to już nie jest nawet smieszne ;^)
Według karty katalogowej można było zastosować, GDWK 11/100 i 10/80/19 ponieważ ich rekomendowana częstotliwość podziału to 2800Hz.
Co w takim razie stało na przeszkodzie w wykorzystaniu tychże przetworników, które dają możliwość przesunięcia podziału niżej i eliminacji "break-up'u" GDM-a ? Też liniowy moduł impedancji ? ;^)
Według karty katalogowej można było zastosować, GDWK 11/100 i 10/80/19 ponieważ ich rekomendowana częstotliwość podziału to 2800Hz.
Co w takim razie stało na przeszkodzie w wykorzystaniu tychże przetworników, które dają możliwość przesunięcia podziału niżej i eliminacji "break-up'u" GDM-a ? Też liniowy moduł impedancji ? ;^)
Ostatnia edycja:
Przyczyny wykonania zwrotnicy w takiej a nie innej konfiguracji były trzy:
1) Wytrzymałość mocowa głośnika GDWK 9/80/1. Wyższa częstotliwość podziału to bezpieczniejsze warunki pracy. Głośnik pracuje bez dzielnika oporowego więc chroni go jedynie filtr trzeciego rzędu i ewentualnie limiter w postaci żarówki samochodowej 12V/21W przed filtrem, którego ja akurat w swoim zestawie nie zamontowałem ponieważ w miarę możliwości staram się nie wysterowywać go pełną mocą wzmacniacza.
2) Zagadnienia dotyczące przebiegu fazowego. Przy tej częstotliwości podziału (5000 Hz) stosunkowo łatwo można uzyskać zgodny przebieg faz sygnału głośnika średniotonowego i wysokotonowego bez dodatkowych komplikacji układu, filtrów wszechprzepustowych LC, zmiany głębokości montażu głośnika wysokotonowego względem średniotonowego, itp.
3) Względy estetyczne. Głośnik GDWK 9/80/1 ładnie prezentuje się z dedykowanym pierścieniem wykonanym z diamentowanego aluminium pomalowanego na czarno. Załączyłem w pierwszej wiadomości rysunek techniczny, który można przesłać do Tonsilu celem zamówienia wykonania takiego pierścienia. Tego typu rozwiązanie było stosowane w fabrycznych zestawach głośnikowych "Dynamic Speaker" HX-100.
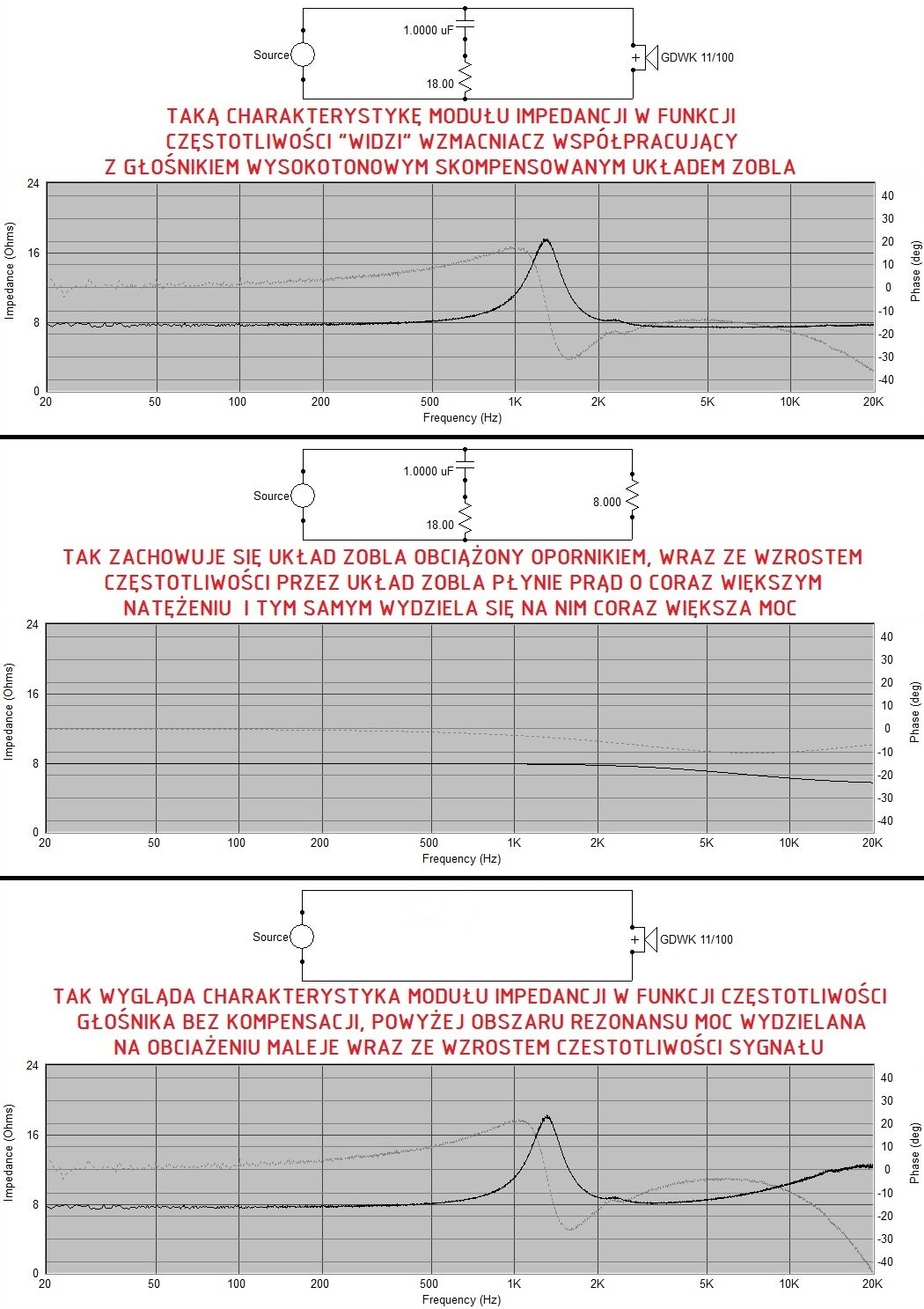
Tutaj ma Pan artykuł z opisem zestawu głośnikowego, w którym zastosowano niższą częstotliwość podziału (4000 Hz), z tym że wymaga to zamiany głośnika średniotonowego na GDM 18/40/1, wysokotonowego na GDWK 11/100 oraz dodatkowo wpuszczenia głośnika wysokotonowego w głąb ekranu zestawu celem wyrównania charakterystyk fazowo-częstotliwościowych. W zwrotnicy w gałęzi GDWK jest nawet przewidziany opornik, który pełni trzy funkcje na raz. Wyrównuje mianowicie charakterystykę poziomu ciśnienia akustyczego w funkcji częstotliwości, prostuje odchylenie w dół poniżej wartości znamionowej na charakterystyce modułu impedancji w funkcji częstotliwości oraz zabezpiecza głośnik wysokotonowy przed przeciążeniem. Dodatkowo GDWK jest chroniony zastosowaniem połączenia kaskadowego, w którym gałąź wysokotonowa wyprowadzona jest z części filtra pasmowoprzepustowego głośnika średniotonowego:
https://sigma-not.pl/publikacja-788...strukcje-technologie-zastosowania-2013-8.html
1) Wytrzymałość mocowa głośnika GDWK 9/80/1. Wyższa częstotliwość podziału to bezpieczniejsze warunki pracy. Głośnik pracuje bez dzielnika oporowego więc chroni go jedynie filtr trzeciego rzędu i ewentualnie limiter w postaci żarówki samochodowej 12V/21W przed filtrem, którego ja akurat w swoim zestawie nie zamontowałem ponieważ w miarę możliwości staram się nie wysterowywać go pełną mocą wzmacniacza.
2) Zagadnienia dotyczące przebiegu fazowego. Przy tej częstotliwości podziału (5000 Hz) stosunkowo łatwo można uzyskać zgodny przebieg faz sygnału głośnika średniotonowego i wysokotonowego bez dodatkowych komplikacji układu, filtrów wszechprzepustowych LC, zmiany głębokości montażu głośnika wysokotonowego względem średniotonowego, itp.
3) Względy estetyczne. Głośnik GDWK 9/80/1 ładnie prezentuje się z dedykowanym pierścieniem wykonanym z diamentowanego aluminium pomalowanego na czarno. Załączyłem w pierwszej wiadomości rysunek techniczny, który można przesłać do Tonsilu celem zamówienia wykonania takiego pierścienia. Tego typu rozwiązanie było stosowane w fabrycznych zestawach głośnikowych "Dynamic Speaker" HX-100.
Tutaj ma Pan artykuł z opisem zestawu głośnikowego, w którym zastosowano niższą częstotliwość podziału (4000 Hz), z tym że wymaga to zamiany głośnika średniotonowego na GDM 18/40/1, wysokotonowego na GDWK 11/100 oraz dodatkowo wpuszczenia głośnika wysokotonowego w głąb ekranu zestawu celem wyrównania charakterystyk fazowo-częstotliwościowych. W zwrotnicy w gałęzi GDWK jest nawet przewidziany opornik, który pełni trzy funkcje na raz. Wyrównuje mianowicie charakterystykę poziomu ciśnienia akustyczego w funkcji częstotliwości, prostuje odchylenie w dół poniżej wartości znamionowej na charakterystyce modułu impedancji w funkcji częstotliwości oraz zabezpiecza głośnik wysokotonowy przed przeciążeniem. Dodatkowo GDWK jest chroniony zastosowaniem połączenia kaskadowego, w którym gałąź wysokotonowa wyprowadzona jest z części filtra pasmowoprzepustowego głośnika średniotonowego:
https://sigma-not.pl/publikacja-788...strukcje-technologie-zastosowania-2013-8.html
Jeśli komuś bardzo zależy na tym, żeby się to wszystko fazowo idealnie zgadzało to należy zwiększyć pojemność kondensatora C1 we filtrze GDN-a z 56 uF na 100 uF:
Wszystkie głośniki podłączone synfazowo:
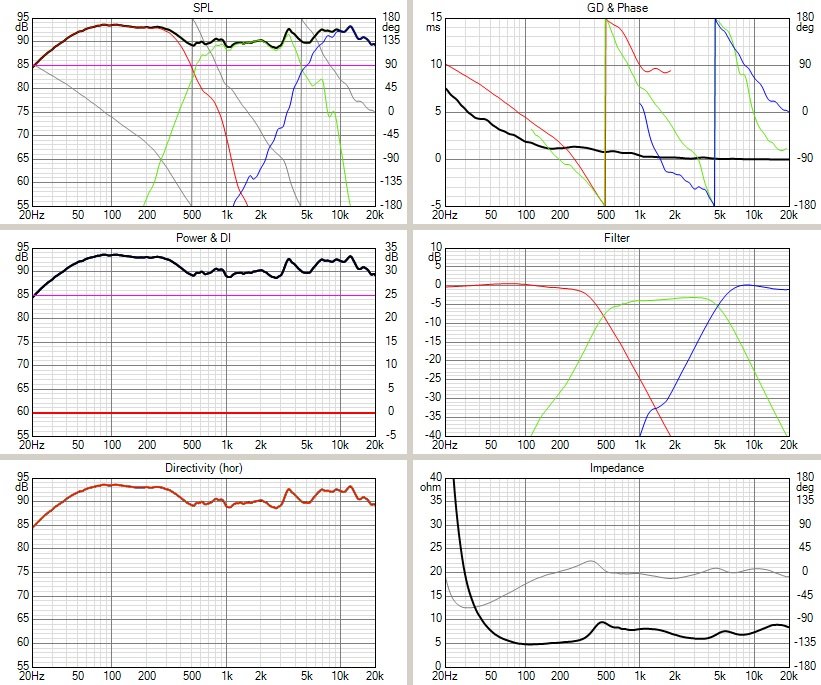
GDM 18/80 podłączony afazowo:
Ale każdy kij ma dwa końce. Taki zabieg spowoduje zjazd minimum na charakterystyce modułu impedancji w funkcji częstotliwości z siedmiu omów na pięć omów a to minimum przypada akurat w obszarze, gdzie przykłada się do zestawu sygnał o dużej mocy i może to doprowadzić do przeciążenia stopnia końcowego wzmacniacza podczas pracy na pełnym wysterowaniu. Coś za coś.
Wszystkie głośniki podłączone synfazowo:
GDM 18/80 podłączony afazowo:
Ale każdy kij ma dwa końce. Taki zabieg spowoduje zjazd minimum na charakterystyce modułu impedancji w funkcji częstotliwości z siedmiu omów na pięć omów a to minimum przypada akurat w obszarze, gdzie przykłada się do zestawu sygnał o dużej mocy i może to doprowadzić do przeciążenia stopnia końcowego wzmacniacza podczas pracy na pełnym wysterowaniu. Coś za coś.
Załączniki
Nie ma sensu kruszyć kopii o to, która opcja lepsza ponieważ w projektowaniu filtrów rozwidlających do zespołów głośnikowych zawsze trzeba iść na jakieś kompromisy. Albo będzie w pełni prawidłowo od strony akustycznej kosztem pogorszenia parametrów elektrycznych. Albo będzie w pełni prawidłowo od strony elektrycznej kosztem pogorszenia parametrów akustycznych. Obciążenie filtrów głośnikami dynamicznymi prawie zawsze powoduje różne kłopoty i w praktyce trudno jest dobrać do siebie trzy głośniki, które będą chciały ze sobą współpracować bez problemów z filtracją. W książce opisałem różne manewry, które pozwalają wyeliminować część tych problemów, tym niemniej zasada odchylenia +/- 15% od wartości znamionowej modułu impedancji poza obszarem rezonansu bądź rezonansów głośnika niskotonowego w obudowie jest umowna. Ja tej zasady akurat przestrzegam i projektuję filtry właśnie w taki sposób. Ma to swoje zalety, ma też wady. To już czytelnicy ocenią. Tym niemniej książka nie jest wyrocznią i każdy musi polegać na własnym rozumie i wyczuciu konstruktorskim. To jest tylko wprowadzenie do tematu, żeby w ogóle "poczuć bluesa" i dowiedzieć się jak te filtry działają i o co w tym wszystkim chodzi.
Główny problem ze zwrotnicami głośnikowymi polega na tym, że te filtry obliczane są dla obciążenia o charakterze rezystancyjnym, tzn. takim, w którym moduł impedancji obiektu obciążającego wyjście filtra dla każdej częstotliwości pasma akustycznego przyjmuje stałą wartość (np. 8 omów). Rzeczywiste obciążenie ma charakter reaktancyjny wynikający ze schematu zastępczego głośnika dynamicznego. Wykres podzielić można na cztery obszary:
1) Obszar poniżej rezonansu, gdzie moduł impedancji przyjmuje wartość równą w przybliżeniu rezystancji szeregowej uzwojenia cewki głośnika przy pobudzeniu stałoprądowym.
2) Obszar rezonansu, w którym moduł impedancji najpierw przyrasta osiągając lokalne ekstremum a następnie opada do poziomu tzw. impedancji znamionowej.
3) Obszar w którym moduł impedancji utrzymuje wartość impedancji znamionowej.
4) Obszar, w którym następuje przyrost wartości modułu impedancji na skutek udziału składowej reaktancyjnej (w tym przypadku pochodzącej od induktancji czyli reaktancji indukcyjnej uzwojenia cewki głośnika) wraz ze wzrostem częstotliwości.
Dla przykładu charakterystyka modułu impedancji funkcji częstotliwości głośnika GDM 18/40/1:
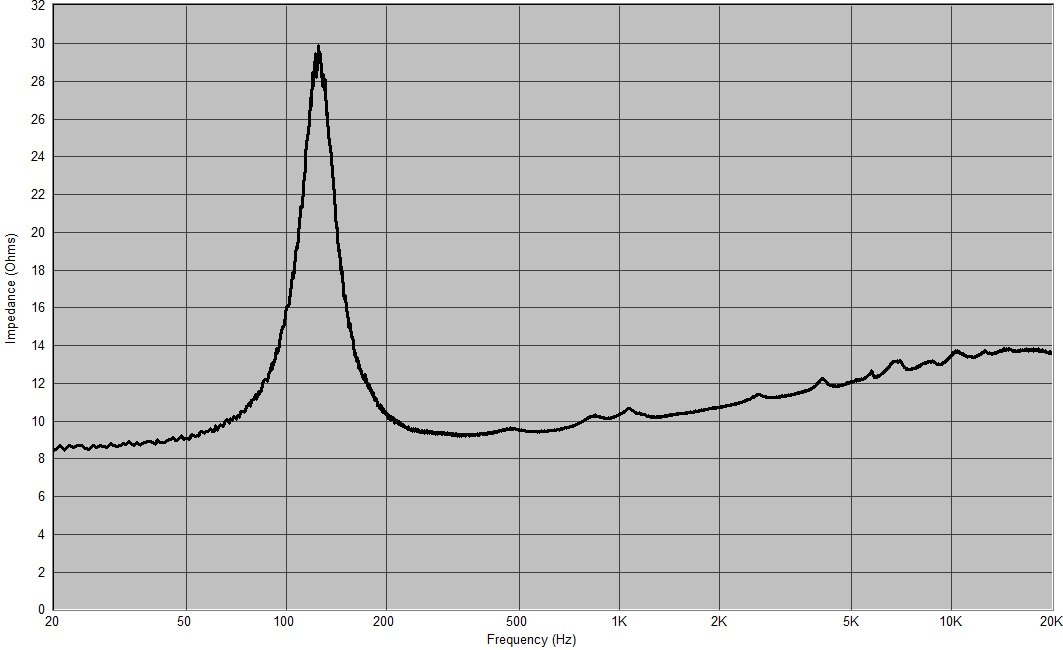
No i teraz możemy przeprowadzić eksperyment mający na celu uświadomienie sobie, w jaki sposób zachowa się filtr pasmowoprzepustowy pierwszego rzędu obciążony oporem stałym i rzeczywistym przetwornikiem. W ramach przykładu przyjmujemy obciążenie ośmioomowe i częstotliwości podziału fd = 200 Hz oraz fg = 2000 Hz.
Filtr obciążony oporem stałym:
Filtr obciążony głośnikiem dynamicznym GDM 18/40/1:
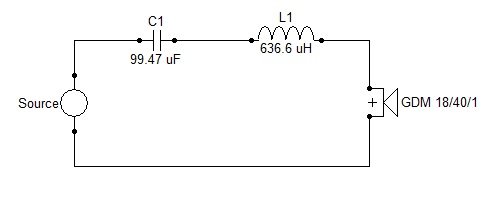
Dla uproszczenia przyjmujemy, że charakterystyka poziomu ciśnienia akustycznego w funkcji częstotliwości głośnika jest linią prostą na poziomie 0 dB:
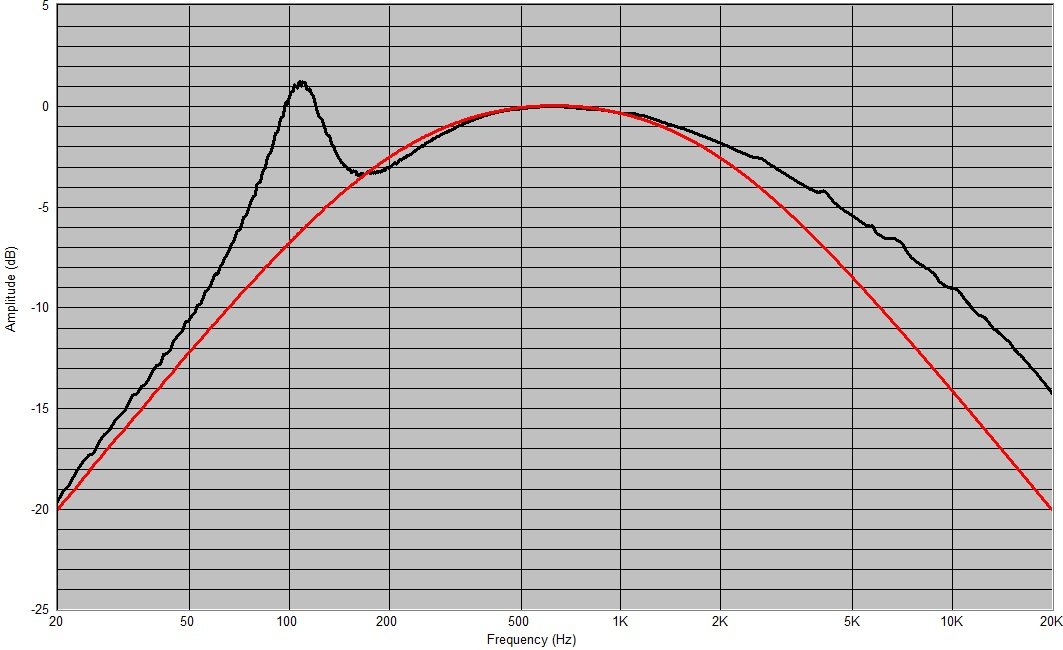
Linia czerwona to filtr obciążony oporem stałym, linia czarna to filtr obciążony rzeczywistym głośnikiem dynamicznym.
Obserwacje:
1) W rezonansie filtr w ogóle nie działa. Wynika to z faktu, że ustaliliśmy fd bardzo blisko częstotliwości rezonansowej głośnika i zastosowaliśmy filtr pierwszego rzędu o nachyleniu 6 dB/okt. Moduł impedancji w szczycie stanowi wielokrotność wartości modułu impedancji, dla którego został zaprojektowany filtr.
2) W obszarze przepustowym filtr działa mniej więcej zgodnie z przewidywaniami ponieważ obszar ten pokrywa się z obszarem, w którym moduł impedancji utrzymuje wartość impedancji znamionowej.
3) W obszarze zaporowym powyżej fg wraz ze wzrostem częstotliwości filtr działa coraz słabiej. Wynika to z faktu stopniowego przyrostu wartości modułu impedancji w funkcji częstotliwości na tym obszarze charakterystyki.
Środki zaradcze:
1) Stosowanie fd w bezpiecznym oddaleniu od częstotliwości rezonansowej głośnika (dotyczy to szczególnie głośników wysokotonowych).
2) Zastosowanie filtrów wyższego rzędu o nachyleniu 12, 18 lub 24 dB/okt.
3) W przypadku gdy chcemy zastosować niższy podział lub mniejsze nachylenie filtra musimy skompensować charakterystykę modułu impedancji w funkcji częstotliwości w obszarze rezonansu przy pomocy pułapki rezonansowej RLC (taki zabieg to raczej ostateczność).
4) W przypadku filtrów dolnoprzepustowych spadek efektywności działania filtra wraz ze wzrostem częstotliwości załatwiamy obwodem kompensacyjnym Zobla lub optymalizacją wyliczonych wcześniej elementów filtra (np. na drodze symulacji w programach komputerowych typu Speaker Workshop lub VituixCAD).
W rzeczywistości dochodzą nam jeszcze sprawy związane z nieliniowym kształtem charakterystyki poziomu ciśnienia akustycznego głośnika dynamicznego w funkcji częstotliwości. Tutaj jednak przeanalizowałem tylko parametry elektryczne obciążenia oraz ich wpływ na działanie filtra aby zjawiska te były lepiej zrozumiałe dla początkujących konstruktorów.
1) Obszar poniżej rezonansu, gdzie moduł impedancji przyjmuje wartość równą w przybliżeniu rezystancji szeregowej uzwojenia cewki głośnika przy pobudzeniu stałoprądowym.
2) Obszar rezonansu, w którym moduł impedancji najpierw przyrasta osiągając lokalne ekstremum a następnie opada do poziomu tzw. impedancji znamionowej.
3) Obszar w którym moduł impedancji utrzymuje wartość impedancji znamionowej.
4) Obszar, w którym następuje przyrost wartości modułu impedancji na skutek udziału składowej reaktancyjnej (w tym przypadku pochodzącej od induktancji czyli reaktancji indukcyjnej uzwojenia cewki głośnika) wraz ze wzrostem częstotliwości.
Dla przykładu charakterystyka modułu impedancji funkcji częstotliwości głośnika GDM 18/40/1:
No i teraz możemy przeprowadzić eksperyment mający na celu uświadomienie sobie, w jaki sposób zachowa się filtr pasmowoprzepustowy pierwszego rzędu obciążony oporem stałym i rzeczywistym przetwornikiem. W ramach przykładu przyjmujemy obciążenie ośmioomowe i częstotliwości podziału fd = 200 Hz oraz fg = 2000 Hz.
Filtr obciążony oporem stałym:
Filtr obciążony głośnikiem dynamicznym GDM 18/40/1:
Dla uproszczenia przyjmujemy, że charakterystyka poziomu ciśnienia akustycznego w funkcji częstotliwości głośnika jest linią prostą na poziomie 0 dB:
Linia czerwona to filtr obciążony oporem stałym, linia czarna to filtr obciążony rzeczywistym głośnikiem dynamicznym.
Obserwacje:
1) W rezonansie filtr w ogóle nie działa. Wynika to z faktu, że ustaliliśmy fd bardzo blisko częstotliwości rezonansowej głośnika i zastosowaliśmy filtr pierwszego rzędu o nachyleniu 6 dB/okt. Moduł impedancji w szczycie stanowi wielokrotność wartości modułu impedancji, dla którego został zaprojektowany filtr.
2) W obszarze przepustowym filtr działa mniej więcej zgodnie z przewidywaniami ponieważ obszar ten pokrywa się z obszarem, w którym moduł impedancji utrzymuje wartość impedancji znamionowej.
3) W obszarze zaporowym powyżej fg wraz ze wzrostem częstotliwości filtr działa coraz słabiej. Wynika to z faktu stopniowego przyrostu wartości modułu impedancji w funkcji częstotliwości na tym obszarze charakterystyki.
Środki zaradcze:
1) Stosowanie fd w bezpiecznym oddaleniu od częstotliwości rezonansowej głośnika (dotyczy to szczególnie głośników wysokotonowych).
2) Zastosowanie filtrów wyższego rzędu o nachyleniu 12, 18 lub 24 dB/okt.
3) W przypadku gdy chcemy zastosować niższy podział lub mniejsze nachylenie filtra musimy skompensować charakterystykę modułu impedancji w funkcji częstotliwości w obszarze rezonansu przy pomocy pułapki rezonansowej RLC (taki zabieg to raczej ostateczność).
4) W przypadku filtrów dolnoprzepustowych spadek efektywności działania filtra wraz ze wzrostem częstotliwości załatwiamy obwodem kompensacyjnym Zobla lub optymalizacją wyliczonych wcześniej elementów filtra (np. na drodze symulacji w programach komputerowych typu Speaker Workshop lub VituixCAD).
W rzeczywistości dochodzą nam jeszcze sprawy związane z nieliniowym kształtem charakterystyki poziomu ciśnienia akustycznego głośnika dynamicznego w funkcji częstotliwości. Tutaj jednak przeanalizowałem tylko parametry elektryczne obciążenia oraz ich wpływ na działanie filtra aby zjawiska te były lepiej zrozumiałe dla początkujących konstruktorów.
Ostatnia edycja:
Spoko, ładna symulacja, faktycznie ładnie widać.
Ale raczej nikt nie liczy filtrów ręcznie dla obciążenia rezystancyjnego, bo i po co? Wprawdzie nawet na forum jest artykuł jak to zrobić, ale w gruncie rzeczy już nikt tak nie robi.
Algorytm wygląda inaczej, symulujemy w sofcie w oparciu o zmierzony moduł impedancji. Oczywiście że kompensacja piku impedancji jest stosowana chyba, że akurat tak wychodzi że filtr pozwala jej nie stosować bo i tak się przecież zdarza.
Ale raczej nikt nie liczy filtrów ręcznie dla obciążenia rezystancyjnego, bo i po co? Wprawdzie nawet na forum jest artykuł jak to zrobić, ale w gruncie rzeczy już nikt tak nie robi.
Algorytm wygląda inaczej, symulujemy w sofcie w oparciu o zmierzony moduł impedancji. Oczywiście że kompensacja piku impedancji jest stosowana chyba, że akurat tak wychodzi że filtr pozwala jej nie stosować bo i tak się przecież zdarza.
I tak pewnie nie dojdziemy do porozumienia. W książce przedstawiłem swój SUBIEKTYWNY pogląd mówiący o tym, że ważne jest prawidłowe opracowanie projektu zwrotnicy od strony ELEKTRYCZNEJ. We wcześniejszych postach starałem się uświadomić Państwu czym grozi zmuszanie zespołu głośników do pełnego zgrania fazowego. Da się to zrobić ale w życiu zawsze jest coś za coś. Głośnik dynamiczny cewkowy jest bardzo niewdzięcznym rodzajem obciążenia filtra. Wynika to z jego zasady działania. Chyba tylko głośniki wstęgowe dają się łatwo filtrować ponieważ ich charakterystyka modułu impedancji w funkcji częstotliwości jest linią prostą równą w przybliżeniu rezystancji folii drgającej w polu magnetycznym. Spór pozostanie nierozstrzygnięty. No ale w książce trzeba było napisać tak a nie inaczej ponieważ czytelnik musi mieć jakieś pojęcie o tym jak to w ogóle działa i jakie są konsekwencje poszczególnych zabiegów konstrukcyjnych. To jest przede wszystkim książka dla młodzieży z technikum elektronicznego. Bardziej zaawansowanym projektantom polecam książki profesorów Żyszkowskiego i Dobruckiego, na które powołuję się m.in. w bibliografii.
E, no nie bądź takim pesymistą. Jeśli mówimy o projektowaniu kolumn. Bo jeśli o promocji książki, to nie jestem zainteresowany tematem.
Z moich doświadczeń, znacznie bardziej wolę dobre, szerokie zgranie fazowe. Jeśli chodzi o moje preferencje, to stereofonia to jest to
Nawet mogę wybaczyć nie za duże rozjazdy na charakterystyce częstotliwościowej, byle sterefonia była wciągająca. Masz rację, że to kwestia kompromisu, co kto woli. Ja nie mam problemu z nierównym wykresem impedancji.
To nie spór, nie mam misji cię przekonać. Wolę to traktować jak dyskusję czy zwyczajną rozmowę na temat.
Każda zwrotnica to pewnego rodzaju kompromis. Ja to zrobiłem tak żeby fazowo się to zgadzało na drugiej częstotliwości podziału ponieważ tam wszelkie rozjazdy są wyraźniej słyszalne z punktu widzenia użytkownika. Wypadkowa charakterystyka modułu impedancji w funkcji częstotliwości poza obszarem rezonansów głośnika niskotonowego w obudowie basrefleks mieści się w tym zestawie w granicach od 6,8 oma do 9,2 oma. Na pierwszej częstotliwości podziału mamy odkłonienie wynoszące około 40 stopni ale w tym zakresie częstotliwości nie jest to aż tak wyraźnie słyszalne.